share
The Integral Sphere: A Mathematical Mandala of Reality
Thomas J. McFarlane
June 2004
www.integralscience.org
The web address of this article is http://www.integralscience.org/sphere.html
Copyright 2004 Thomas J McFarlane
(Note: This document contains HTML 4.0 character entities.)
Abstract. This article presents a dynamic mathematical mandala which can be seen as an integral model of reality. In contrast with conventional two-dimensional mandalas, the mandala described here is a sphere in three (or more) dimensions. Moreover, through a process of breaking the perfect symmetry of the three-dimensional sphere and then projecting the sphere onto a plane, the sphere is related to conventional linear, planar mandalas and unfolds their implicit archetypal structures. For example, a mandala with many similarities to Ken Wilber's Four Quadrant model of the Kosmos is unfolded as a special case of the spherical mandala. A four-dimensional integral sphere also contains Wilber's nested spheres as a special case. Higher dimensional spheres can be used to represent additional aspects of existence. The paper also shows how the present model provides a tool for facilitating complex thinking with fundamental categories, revealing how they interpenetrate and transform into each other.
Introduction
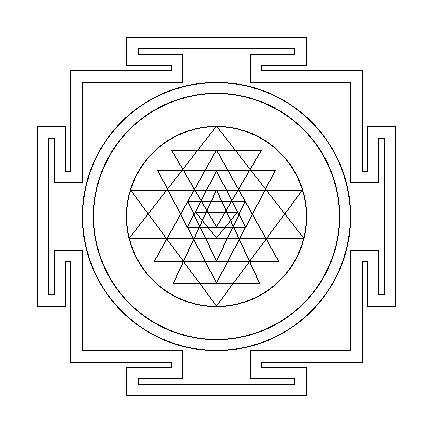 In nearly every culture, mandalas have been used as symbolic representations of reality (Argüelles, 1972; see also Cunningham's Mandala Project). Typically, a mandala contains symbolic icons which have special meaning, and these symbols are arranged to show their places in the cosmos. Some mandalas, such as the sri yantra, contain geometric rather than iconic symbols and the spatial relationships between these geometric symbols carry the primary symbolic meaning. In addition to representing the cosmos in a compact, symbolic form, mandalas are used as tools for contemplation and inner transformation. Meditation upon a mandala, for example, can reveal deeper relationships between various parts of reality and help one to attain a more integral vision of oneself and the cosmos.
In nearly every culture, mandalas have been used as symbolic representations of reality (Argüelles, 1972; see also Cunningham's Mandala Project). Typically, a mandala contains symbolic icons which have special meaning, and these symbols are arranged to show their places in the cosmos. Some mandalas, such as the sri yantra, contain geometric rather than iconic symbols and the spatial relationships between these geometric symbols carry the primary symbolic meaning. In addition to representing the cosmos in a compact, symbolic form, mandalas are used as tools for contemplation and inner transformation. Meditation upon a mandala, for example, can reveal deeper relationships between various parts of reality and help one to attain a more integral vision of oneself and the cosmos.
Nearly every mandala is represented in a two-dimensional plane. Often the plane is divided into the four cardinal directions and has a center with concentric circles emanating outward.
However, a some mystics have used the sphere as a symbol to express their profound insight into Reality. For example, the Tibetan Buddhist Chögyal Namakhai Norbu writes:
"Total Sphere" ... is a synonym of Dzogpa Chenpo. In short, what this really means is that the state of consciousness has no beginning or end and is free of limits, like an immense sphere. (Chögyal Namakhai Norbu, p. 93, Supreme Source)
Similarly, the Greek philosopher Parmenides used the sphere as a symbol to express his deepest insight into the nature of Reality:
Being...is ungenerated and indestructible, whole, of one kind and unwavering, and complete. Nor was it, nor will it be, since now it is, all together, one, complete. ...It is completed on all sides, like the bulk of a well-rounded ball, equal in every way from the middle. For it must not be at all greater or smaller here or there. (Parmenides, p. 134-135, Early Greek Philosophy)
The Christian mystical philosopher Nicholas of Cusa also uses the sphere as the most profound symbol for God, or Ultimate Reality:
Others who have attempted to depict infinite unity have spoken of God as an infinite circle, but those who have considered the most actual existence of God have affirmed that God is as if an infinite sphere. (Cusa, Selected Spiritual Writings, p. 102)
Why should the sphere be a more perfect symbol of reality than the circle or other two-dimensional mandalas? What symbolic meaning is contained in the sphere? In the sections that follow, we will take a deeper look into this symbol and unfold the wonderful and beautiful teachings it contains. In order to illustrate the features of the spherical mandala most clearly, we will construct it in stages. First we will present a one-dimensional mandala that consists of a single line plus a single point transcending the line. We will then unpack the rich symbolic power of this linear mandala. Next, the line is seen from a different point of view to be a circle. This circular mandala reveals even deeper meaning that was hidden from the linear mandala. Next we generalize the line to a plane and the circle to a sphere to obtain the higher-dimensional analogues of these mandalas. In addition to containing all the symbolic content of the lower-dimensional mandalas, the sphere provides added dimensions and corresponding riches of symbolic interpretation.
The Line and the Circle
Experience is an on-going arising and passing away of sensations, thoughts, feelings, and other ephemeral phenomena, all appearing and disappearing in a space of consciousness throughout our lives. There is an intuition, however, of an awareness or knower that is somehow above it all and unchanging, providing a sense of continuity to our consciousness throughout all the changes in experience. It is the bare sense of awareness that is present when we first wake up, before thoughts of who we are or where we are have arisen. Prior to the variant multitude of the known, there is an invariant unity of the knower. In short, prior to the world of objects, there is a subject. Thus, we begin with this primordial distinction between the Transcendent One and the Manifest Many. Although this terminology is taken from the Neoplatonic tradition (Proclus, 1987; Plotinus, 1991), this same distinction goes by other names in different traditions. In the Buddhist tradition, this is the distinction between unborn naked awareness and the various phenomena arising in awareness (Norbu, 1999). In Advaita Vedanta this is the distinction between the Subject, or Atman, and the manifold objects in the world of experience (Shankara, 1978). The singular Subject to consciousness transcends the phenomenal world of manifold objects in the sense that this formless Awareness is never itself a phenomenal object arising and passing away as any content in consciousness. The formless Awareness may be symbolically represented as another order of being transcending all content.
The Line
We can represent the manifest world of forms as a horizontal line consisting of an infinite collection of points, each symbolizing the potential presence of a phenomenal object in consciousness. The arising and passing of forms is a dance of points along this line. The unborn and undying subjective awareness, which is not a manifest object, is not a point on this line of objective phenomena, so it is represented as a point separated from the line, a singular point "at infinity." This point is not any "thing" because it is the knower of all things. It is a no-thing that knows things. In contrast, anything arising in awareness is a point on the line, an object of awareness, a thing that is known.
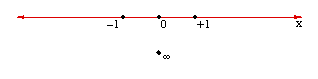 Notice that there is a discontinuity between the manifest line and the unmanifest point at infinity. No movement along the line, no matter how far out, will ever reach the transcendent point. Conversely, the transcendent point can never appear among the objects of the world. To illustrate this mathematically, a point on the line can be called the origin, and the line can be given a metric so that one can measure distances from the origin. The line then becomes a number line, such as the real number line, where each point corresponds to a number. The origin corresponds to zero, points to the right of the origin correspond to the positive numbers, and points to the left of the origin correspond to negative numbers. Points further and further from the origin correspond to larger and larger numbers. No matter how far away the point, though, it will always correspond to some finite number. Just as infinity is not a finite number, the point at infinity is not a point on the line. It transcends the points on the line, just as infinity transcends all finite numbers.
Notice that there is a discontinuity between the manifest line and the unmanifest point at infinity. No movement along the line, no matter how far out, will ever reach the transcendent point. Conversely, the transcendent point can never appear among the objects of the world. To illustrate this mathematically, a point on the line can be called the origin, and the line can be given a metric so that one can measure distances from the origin. The line then becomes a number line, such as the real number line, where each point corresponds to a number. The origin corresponds to zero, points to the right of the origin correspond to the positive numbers, and points to the left of the origin correspond to negative numbers. Points further and further from the origin correspond to larger and larger numbers. No matter how far away the point, though, it will always correspond to some finite number. Just as infinity is not a finite number, the point at infinity is not a point on the line. It transcends the points on the line, just as infinity transcends all finite numbers.
Because the subject never becomes an object, the uncreated is never created, it is often forgotten or ignored. The no-thing becomes a nothing. The world of created things then appears to be the entire reality, leaving nothing out. The line without the point at infinity represents all of creation, but leaves out the transcendent source. It is a symbol for all form, but ignores the formless. It displays the world of objects, but forgets the subject. The linear mandala reduces Reality to the finite and blinds us to the infinite, limits us to the variable phenomena by leaving out the invariant awareness. An integral model of reality should therefore explicitly represent what transcends the linear world of objects, and resist the temptation to leave it out.
Although the transcendent point at infinity should be included in any complete model of reality, because it is a simple formless point it has no structure. The points on the line, in contrast, can be given a structure. What are the relationships between objects in experience? What different kinds of objects are there? What are their distinguishing properties? How do they behave? These questions can be given meaning when applied to the manifest world. As a result, elaborate mandalas have been developed to provide answers to these questions. We will focus here on just the most fundamental and universal themes.
Grading the Linear World
The various spiritual traditions, and the perennial philosophy in particular (Smith, 1977), teach that the manifest world is a graded reality. Just as the unmanifest One is distinguished from the manifest Many, so the variable phenomena of the Many are distinguished from each other according to their degree of reality or value. Every cosmology has some such grading, some way of saying what kinds of things have more value and more reality. For example, one way of grading things is to notice that what endures is more real and valuable than what quickly perishes. A car that breaks down and is useless a few months after it is made is not as valuable as a car that runs for many years. An experience of something unusual is more likely to be considered real if it persists day after day. What is real and valuable, in short, is what is most invariant under changes in time, place, and circumstance.
Just as a grading on the linear world of phenomena requires some criterion for assigning degrees of value or reality, so a measure of magnitude on the line requires a metric for assigning numerical values to points. This metric is provided by the conventional Euclidean distance, producing the familiar real number line. The numerical magnitude assigned to each point then corresponds to its degree of reality value. The origin has zero magnitude and thus no value, while points further away from the origin have increasing (positive or negative) magnitude and thus increasing value and reality. The point at infinity has infinite value.
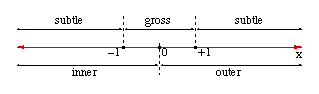 This grading of the points on the line separates them naturally into those near the origin with small values, and those far away from the origin with large values. For example, those points between −1 and +1 can be called gross phenomena or concrete objects. They do not enjoy much invariance and are thus least real and valuable. Those points to the left of −1 and to the right of +1 can be called the subtle phenomena or formal objects. They have high invariance, value, and reality. Note that this distinction between subtle and gross within the realm of objects reflects the primordial distinction between the infinite and the finite. This mirroring of the One/Many distinction in the world of form as the Large/Small distinction is a symbolic representation of the principle "as above, so below" which generates levels of order among phenomena.
This grading of the points on the line separates them naturally into those near the origin with small values, and those far away from the origin with large values. For example, those points between −1 and +1 can be called gross phenomena or concrete objects. They do not enjoy much invariance and are thus least real and valuable. Those points to the left of −1 and to the right of +1 can be called the subtle phenomena or formal objects. They have high invariance, value, and reality. Note that this distinction between subtle and gross within the realm of objects reflects the primordial distinction between the infinite and the finite. This mirroring of the One/Many distinction in the world of form as the Large/Small distinction is a symbolic representation of the principle "as above, so below" which generates levels of order among phenomena.
As one moves further out away from zero (in either direction), one encounters phenomena of increasing subtlety and value. No matter how far one follows the line, however, one will always be at some large but finite distance from zero. In other words, it is impossible to reach infinity in this manner. The One is the Infinitely Real that is entirely beyond and transcending all created phenomena, no matter how subtle.
Inner and Outer Worlds
It will be noticed that the subtle and gross phenomena are naturally divided into two halves: the subtle and gross phenomena on the negative (or left) side of zero, and the subtle and gross phenomena on the positive (right) size of zero. This division of the phenomenal realm into positive and negative, or right and left regions, naturally corresponds to the other fundamental distinction within the created world: the distinction between inner and outer. We have inner experiences such as feeling, thought, and insight, as well as outer experiences of physical objects, subtle energies, the deep order of nature, archetypal or angelic realities, and divine being. Another way of looking at this distinction is between inner modes of knowing (epistemology) and outer modes of being (ontology).
The maxim "as above, so below" may also be interpreted with reference to this distinction. In this case, its meaning is that the ontological levels of being in the exterior cosmos "above" are mirrored "below" in the epistemological levels of knowing in the interior psyche. Gross modes of knowing on the left takes concrete physical entities as its objects on the right. Subtle knowing on the left takes subtle entities as its objects on the right. In general, as Plotinus (1991) states, every type of object requires the corresponding organ of knowledge in order to know it. Thus, while their signs may differ, their magnitudes are the same.
It is significant to observe at this point that interior knowing and corresponding exterior being are both objects in a the fundamental phenomenological sense since they both are part of the line of manifest phenomena. Acts of knowing are cognitive events that come and go in dependence upon the entities that are known. Thus, the inner empirical subject (negative values) and the empirical object (positive values) are both objects (finite values) from the perspective of the transcendental subject (infinity). As finite in nature, the empirical subject and empirical object are both insignificant in comparison with infinity. This accounts for the Buddhist teaching of the ultimate emptiness of both objective things and subjective selves: neither positive side nor negative side of the phenomenal spectrum contains phenomena that have maximal reality. It is especially significant from the spiritual perspective not to confuse the empirical subject, which corresponds roughly to the various phenomena on the left half of the line, with the transcendental subject that is entirely separate from the line. Confusing these two is a fundamental error that spiritual discriminative wisdom is designed to correct (Shankara, 1978).
This linear symbol also has other relevant interpretations. Extending the above considerations, as inner knowing approaches the infinite toward the left, the corresponding outer object approaches the infinite toward the right. In the limit, infinite transcendent knowing at left infinity (Atman) has infinite transcendent being as its object at right infinity (Brahman). These infinities, however, are not properly points on the line, but are infinitely far off, impossible to reach, and in opposite directions. From the perspective of the mandala of the line, therefore, the Vedantic declaration "Atman is Brahman" (Shankara, 1978) is paradoxical. Not only is it inconceivable that one could actually reach the negative infinity of Atman or the positive infinity of Brahman by moving to the left or right on the line, but the identity of positive and negative infinity is even more incomprehensible. It is not surprising, however, that the line, which separates inner and outer and assumes a discontinuous chasm between transcendent and manifest, fails to represent a teaching that identifies these opposites. Remarkably, however, we can creatively use mathematics to view this dualistic linear mandala from a nondual perspective that overcomes these limitations. Thus, we now proceed to the second stage in our construction of the spherical mandala.
The Circle
The mystical theologian Cardinal Nicholas of Cusa regarded mathematics as the best symbol for things divine. He says in De Docta Ignorantia:
Since there is no other approach to a knowledge of things divine than that of symbols, we cannot do better than use mathematical signs on account of their indestructible certitude (Cusa, 1997).
For example, Cusa used geometry to illustrate the identity of the circle and the line. As a circle becomes very large, it appears less curved, much like how the surface of the Earth appears flat to us because it is so large. In the limit where the circle becomes infinite, then the curvature vanishes and the circle coincides with the straight line (Cusa, 1997, p.103).

Cusa's correspondence between the circle and the line, however, has two disadvantages. First, it does not include the point at infinity. Second, it requires passing through an infinite process to form the correspondence. Our approach will therefore differ from Cusa's, even though it follows his basic insight that the apparent opposites of the line circle can be identified. As we will see below, there is another mathematical correspondence between the circle and the line which includes the point at infinity and requires no infinite process. The correspondence is essentially a transformation of our point of view so that the line is seen as a circle. This shift in perspective reveals that the line discontinuously separated from the point at infinity is equivalent to a single continuous circle.
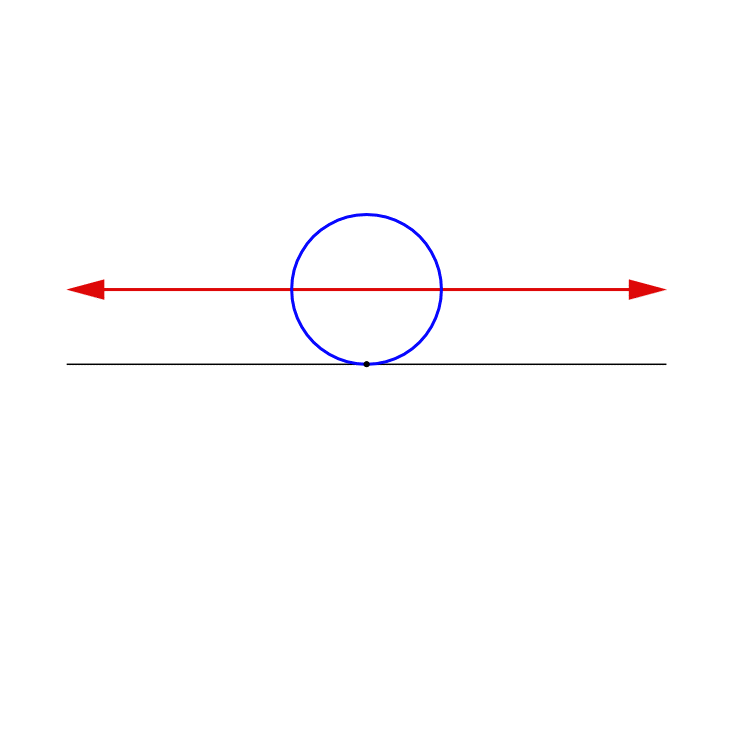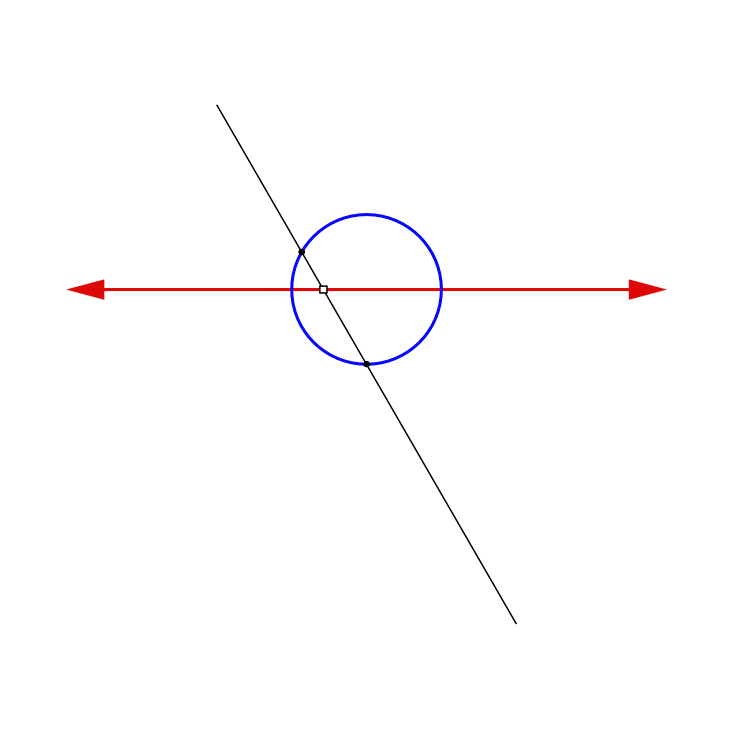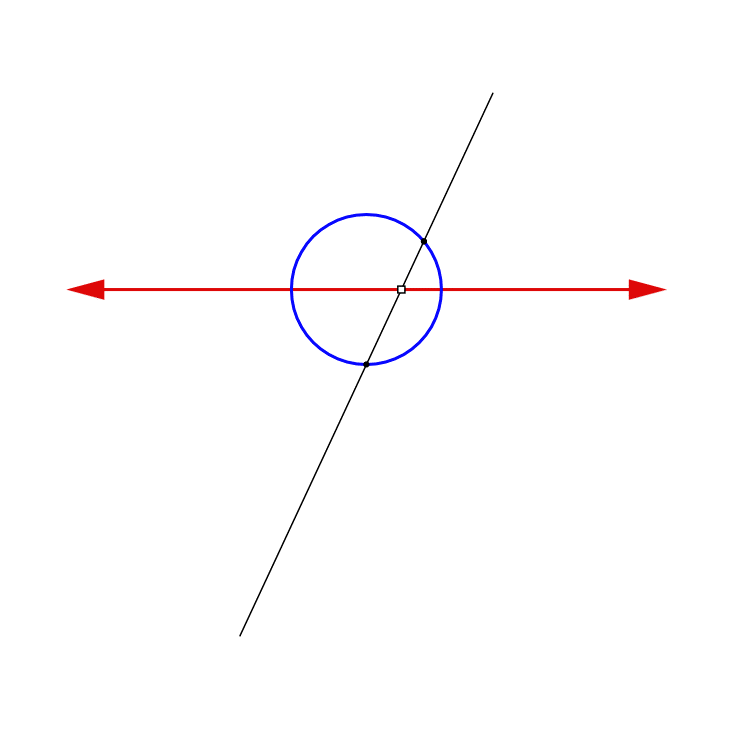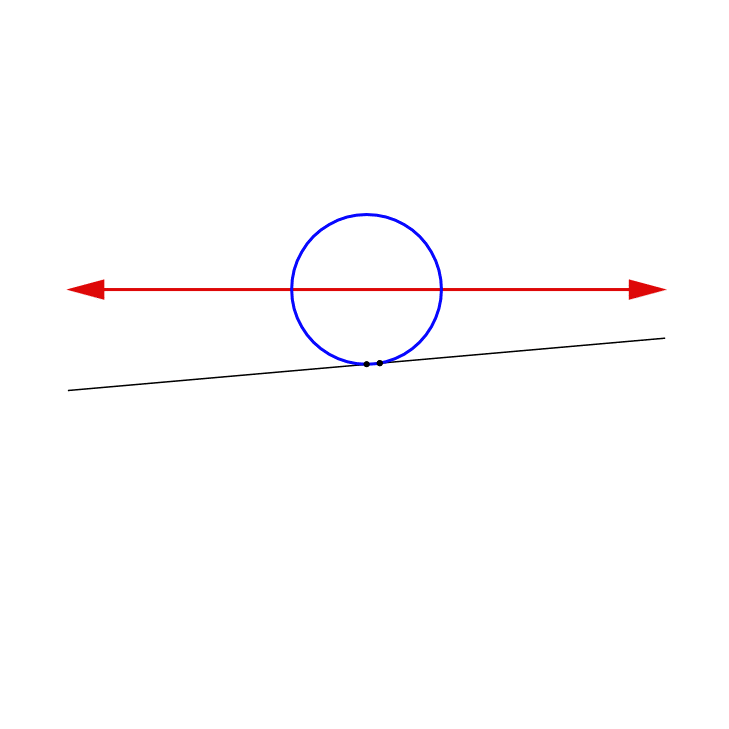
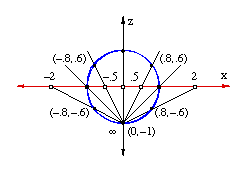
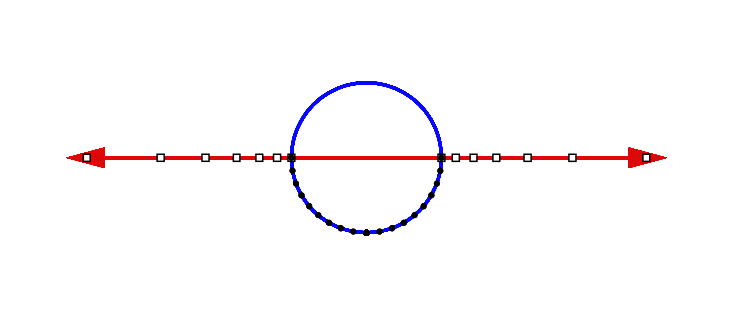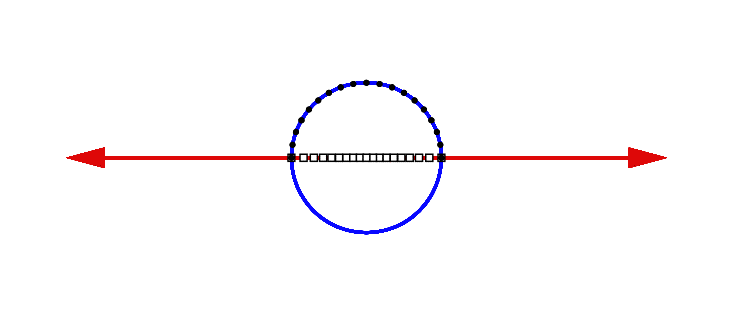
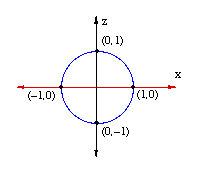 We begin by drawing a vertical z-axis through the line to form a Cartesian coordinate system with the origin of the x-axis at (0,0) and the point at infinity at (0,−1).
Now draw a circle of radius 1 with its center at the origin. Note that the point at infinity corresponds to the bottom point on the circle. In addition, the points (−1,0) and (1,0) on the line correspond to points on the circle. There is thus a self-evident correspondence between three points on the circle and three points of the linear mandala. Moreover, there is a one-to-one correspondence between all the other points on the line and all the other points on the circle. To see this correspondence, imagine a line rotating around the pivot point (0,-1) or, if you prefer, an infinite number of lines radiating outward from (0,-1), the point at infinity. Each of these lines intersects the x-axis at a single point and also intersects the circle at a single point. In other words, each line creates a one-to-one correspondence between a point on the line and a point on the circle. This means that the circle is equivalent to the line.
We begin by drawing a vertical z-axis through the line to form a Cartesian coordinate system with the origin of the x-axis at (0,0) and the point at infinity at (0,−1).
Now draw a circle of radius 1 with its center at the origin. Note that the point at infinity corresponds to the bottom point on the circle. In addition, the points (−1,0) and (1,0) on the line correspond to points on the circle. There is thus a self-evident correspondence between three points on the circle and three points of the linear mandala. Moreover, there is a one-to-one correspondence between all the other points on the line and all the other points on the circle. To see this correspondence, imagine a line rotating around the pivot point (0,-1) or, if you prefer, an infinite number of lines radiating outward from (0,-1), the point at infinity. Each of these lines intersects the x-axis at a single point and also intersects the circle at a single point. In other words, each line creates a one-to-one correspondence between a point on the line and a point on the circle. This means that the circle is equivalent to the line.
 Notice that there is one line that does not actually intersect the x-axis: the horizontal line parallel to the x-axis. This line does, however, intersect the point p at infinity, which is also a unique point on the circle. This line, therefore, matches these two points. Thus, the line plus the point at infinity is equivalent to the entire circle: every point on this circular mandala is matched with one unique point in the linear mandala. Moreover, this correspondence is continuous, meaning that it matches nearby points on the line with nearby points on the circle. In technical terms, this continuous equivalence of the line to the circle is expressed more precisely by saying that the extended real line is homeomorphic to the circle, i.e., they are topologically isomorphic (Singer and Thorpe, 1967). For readers who are interested, the precise details of this correspondence between the line and circle can be found in the mathematical appendix. The essential fact to understand, however, is that the line plus the point at infinity is completely equivalent to the circle, so we are perfectly justified in viewing it as really being a circle.
Notice that there is one line that does not actually intersect the x-axis: the horizontal line parallel to the x-axis. This line does, however, intersect the point p at infinity, which is also a unique point on the circle. This line, therefore, matches these two points. Thus, the line plus the point at infinity is equivalent to the entire circle: every point on this circular mandala is matched with one unique point in the linear mandala. Moreover, this correspondence is continuous, meaning that it matches nearby points on the line with nearby points on the circle. In technical terms, this continuous equivalence of the line to the circle is expressed more precisely by saying that the extended real line is homeomorphic to the circle, i.e., they are topologically isomorphic (Singer and Thorpe, 1967). For readers who are interested, the precise details of this correspondence between the line and circle can be found in the mathematical appendix. The essential fact to understand, however, is that the line plus the point at infinity is completely equivalent to the circle, so we are perfectly justified in viewing it as really being a circle.
Beyond subject and object
Now taking the circle as fundamental we can then view the line as derivative, as arising from the circle through a process of projection. First, a point ∞ on the circle is distinguished from all the other points as a pure subject. Second, rays are imagined to emanate from this point ∞, relating it with other points of the circle, representing objects. Third, these objective points are projected onto a line, representing the severing of the circular whole into an objective world of objects and a transcendent subject. Thus, duality of knower and known, emptiness and form, arises through a process of creating relationship between two points of the same circular reality. The process of projecting this relationship into linear form and forgetting the point at infinity is interpreted as the ignorance that hides the primordial unity of subject and object. Remembering the perspective of the circle reveals the truth that subject and object are aspects of the same continuous whole, with no real distinction between them. From this perspective of the circle, there is pure continuity between the points on the line and the point at infinity, with no discontinuity at all. This shift in perspective, therefore, provides a symbol for the shift from the perspective of discontinuous dualistic consciousness to the perspective of continuous, transcendent consciousness.
In addition, this shift in perspective—seeing the line plus point at infinity as being a circle—reveals as self-evident the teaching that the ultimate subject and the ultimate object are one (e.g., Atman is Brahman). In particular, plus and minus infinity are clearly identified in this circular model, for a point moving infinitely far to the right and a point moving infinitely far to the left correspond to points on the circle approaching the same point at the very bottom of the circle. This coincidence of opposites, as Cusa would call it, cannot be comprehended at the level of the line.
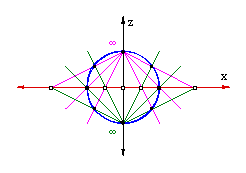 Even deeper yet, we can recognize that the circle has perfect symmetry of all its points: there is no intrinsic difference between the points. No point is inherently privileged or distinguished. Consequently, we are free to select any point as the transcendent subject, or point at infinity. While the linear mandala is fixed to a particular subjective point, the circular mandala invites free transformation, allowing any point on the circle to be regarded as the point from which the manifest world of objects is projected. From the perspective of the circle, it is evident that every point is potentially both a transcendent subject and a manifest object, both emptiness and form. Or, put another way, the transcendent subject is omnipresent and immanent in every object. Prior to the selection of a point at infinity, all points are equally subjective and objective. Moreover, any given point can simultaneously be a subject to which a particular manifest world appears, and an object within the manifest world appearing relative to another subjective point. But, insofar as all the points of the circle are indistinguishable, these subjects are identical. The circle is One continuous unity.
Even deeper yet, we can recognize that the circle has perfect symmetry of all its points: there is no intrinsic difference between the points. No point is inherently privileged or distinguished. Consequently, we are free to select any point as the transcendent subject, or point at infinity. While the linear mandala is fixed to a particular subjective point, the circular mandala invites free transformation, allowing any point on the circle to be regarded as the point from which the manifest world of objects is projected. From the perspective of the circle, it is evident that every point is potentially both a transcendent subject and a manifest object, both emptiness and form. Or, put another way, the transcendent subject is omnipresent and immanent in every object. Prior to the selection of a point at infinity, all points are equally subjective and objective. Moreover, any given point can simultaneously be a subject to which a particular manifest world appears, and an object within the manifest world appearing relative to another subjective point. But, insofar as all the points of the circle are indistinguishable, these subjects are identical. The circle is One continuous unity.
The perspective of the circle reveals that the distinctions inherent in the linear mandala are artifacts of imaginative projection. Instead of a discontinuity between transcendent and manifest, there is continuity. Instead of the ultimate subject and ultimate object being infinite opposites, they are identical. Rather than one point being a privileged and fixed subject, all points are equally endowed with subjectivity. Rather than the world of objects arising in relationship to one fixed subject, various worlds can arise in relation to various subjects. And rather than points being inherently subjective or objective, all are potentially both. As the Buddhists might say, from the perspective of the ultimate truth, everything has "one taste."
Beyond inner and outer, subtle and gross
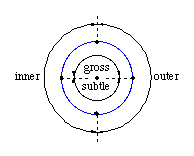 The correspondence between the line and the circle maps the negative valued points on the left side of the line to the left half of the circle and maps the positive valued points on the right side of the line to the right half of the circle. These two halves of the circle correspond to the inner and outer objects of the manifest world. What is less obvious is that the correspondence maps the small valued points near the origin to the upper half of the circle and maps the large valued points to the lower half of the circle. These two halves of the circle correspond to the gross and subtle objects. It is remarkable that while the subtle/gross distinction and the inner/outer distinction appear very differently in the linear mandala, in the circular mandala they have identical form, i.e., both these primordial distinctions arise from the simple act of dividing the world of objects into two halves, the only difference being whether the dividing line is vertical or horizontal.
The correspondence between the line and the circle maps the negative valued points on the left side of the line to the left half of the circle and maps the positive valued points on the right side of the line to the right half of the circle. These two halves of the circle correspond to the inner and outer objects of the manifest world. What is less obvious is that the correspondence maps the small valued points near the origin to the upper half of the circle and maps the large valued points to the lower half of the circle. These two halves of the circle correspond to the gross and subtle objects. It is remarkable that while the subtle/gross distinction and the inner/outer distinction appear very differently in the linear mandala, in the circular mandala they have identical form, i.e., both these primordial distinctions arise from the simple act of dividing the world of objects into two halves, the only difference being whether the dividing line is vertical or horizontal.
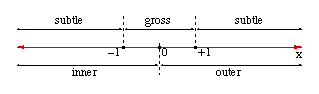 The circle and the line have a left/right reflection symmetry: its form is unchanged if left and right are exchanged. This symmetry shows us that the interior/exterior distinction, i.e., the distinction between the inner and the outer, or between knowing and being, are not ultimately different. In other words, this distinction is an artifact of dividing the circle or line with a vertical line into two halves, calling one half inner and the other half outer. Upon reflection, each inner point on the left is transformed into a corresponding outer point on the right, and vice versa. This reflection symmetry thus illustrates that the knower and known arise together in mutual dependence and are ultimately identical. More specifically, subtle levels of inner knowing correspond to equally subtle levels of outer being, while gross levels of inner knowing correspond to equally gross levels of outer being. This reflection symmetry thus illustrates the principle that every objective level of being requires a corresponding subjective level of knowledge in order to know it (Plotinus, 1991).
The circle and the line have a left/right reflection symmetry: its form is unchanged if left and right are exchanged. This symmetry shows us that the interior/exterior distinction, i.e., the distinction between the inner and the outer, or between knowing and being, are not ultimately different. In other words, this distinction is an artifact of dividing the circle or line with a vertical line into two halves, calling one half inner and the other half outer. Upon reflection, each inner point on the left is transformed into a corresponding outer point on the right, and vice versa. This reflection symmetry thus illustrates that the knower and known arise together in mutual dependence and are ultimately identical. More specifically, subtle levels of inner knowing correspond to equally subtle levels of outer being, while gross levels of inner knowing correspond to equally gross levels of outer being. This reflection symmetry thus illustrates the principle that every objective level of being requires a corresponding subjective level of knowledge in order to know it (Plotinus, 1991).
The circle also has an upper/lower reflection symmetry: its form is invariant when points in the upper half are switched with points in the lower half. Unlike the left/right symmetry, this symmetry is broken when the circle is projected onto the line: there is no reflection symmetry of the line that exchanges small valued points with large valued points. The linear mandala thus conceals the symmetry between subtle and gross levels of reality. As revealed by the circle, there is a symmetry between these sets of points. The exchange of upper and lower points in the circle corresponds to an exchange between small valued points (gross objects) and large valued points (subtle objects). This reflection symmetry thus reveals a mutual dependence and ultimate identity of subtle and gross objects. In particular, the most concrete manifest object at (0,1) is transformed to the infinitely subtle point at infinity (0,−1). This equivalence symbolizes the complete identity of the unmanifest subject with the most concrete of manifest objects (i.e., emptiness is form, and form is emptiness). While paradoxical from the perspective of the line, this identity is obvious from the perspective of the circle. More generally, points of increasing degrees of subtlety correspond with points of increasing degrees of concreteness. This correspondence illustrates that both via positiva and via negativa are mirror images both approaching the ineffable One. The former begins by affirming attributes most closely related to the One, while the latter begins by negating attributes most remote from it (Dionysius, Mystical Theology). These mirror images arise in dependence upon each other and the degree of one corresponds to the degree of the other. The reflection symmetry of the circle reveals that they are equivalent; they are two ways of approaching the One.
Beyond involution and evolution
The upper/lower reflection symmetry also symbolizes the correspondence of the levels of involution (i.e., procession/προοδος) with the levels of evolution (i.e., reversion/επιστροφη). More specifically, the evolutionary process of transcend and include that moves from gross to subtle is the mirror image of the involutionary process of restrict and exclude that moves from subtle to gross. Involution corresponds to a movement from the bottom of the circle to the top, while evolution corresponds to a movement from the top of the circle to the bottom. The upper/lower reflection symmetry inverts these movements, however, and reveals that involution and evolution are two perspectives of the same movement. Another way of understanding this equivalence is to say that involution is a level seen as moving from One to Many, while evolution is the same level seen as moving from Many to One. The shift between these two points of view corresponds to the horizontal reflection. From the perspective of the circle, however, the point is not really moving either way, and yet it can be seen as moving in both ways.
 If we imagine points moving around the circle in both directions, we see them flowing through the processes of involution and evolution, the unfolding of the One to reveal the Many, and an enfolding of the Many back into the One. A point starts at the transcendent Infinite One, manifesting from subtle to gross through the process of involution, then turning around back toward its source in the Infinite One through the process of evolution. Objects are experienced as arising from formlessness into form, and then dissolving back into formlessness. Depending on whether they are experienced as inner or outer objects, their movement is clockwise or counter-clockwise. Since all points on the circle are equivalent due to rotational symmetry, however, there ultimately is no evolution nor involution.
If we imagine points moving around the circle in both directions, we see them flowing through the processes of involution and evolution, the unfolding of the One to reveal the Many, and an enfolding of the Many back into the One. A point starts at the transcendent Infinite One, manifesting from subtle to gross through the process of involution, then turning around back toward its source in the Infinite One through the process of evolution. Objects are experienced as arising from formlessness into form, and then dissolving back into formlessness. Depending on whether they are experienced as inner or outer objects, their movement is clockwise or counter-clockwise. Since all points on the circle are equivalent due to rotational symmetry, however, there ultimately is no evolution nor involution.
The dynamic rotation of the circle, which does not alter it in any way, provides a "moving image of eternity" (Plato) from the perspective of the line. The rotation of the circle is projected onto the line as a movement of points along the length of the line down the hierarchy of involution (movement from infinity to zero) and then up the hierarchy of evolution (movement from zero to infinity). Depending on the direction of rotation, the projected points on the line either move to the right or to the left. Either they arise and dissolve from the infinitely subtle inside or from the infinitely subtle outside. We can follow subtler and subtler phenomenal objects of experience back to their outer source in Brahman, or we can follow subtler and subtler modes of knowing back to their inner source in Atman. Either process implicitly contains the other necessarily since knowing must be fitted to its object (Plotinus). When we see deeper into the interiors, we see deeper into the exteriors. Finally, the emptiness outside merges with the emptiness inside when the line is realized to be a circle and continuity with the point at infinity is unveiled.
Involution and evolution as interpreted above represent the timeless nature of arising and passing, the dance of form and emptiness in the eternal now. These terms also have a more concrete interpretation within the categories of space and time. In particular, within the forms of time and space and matter, the involution process can be seen in the first epoch of the universe during the symmetry breaking process that unfolded the diversity of fundamental physical forces and particles from a unified reality prior to distinctions between the forces, resulting in a vast cosmos of many particles of matter and light. As the cosmos then began the process of evolution, these particles combined and began a process of increasing complexification. This interpretation, however, is an image of the process restricted to the most concrete levels of reality conditioned by time, space, energy, and matter.
The Plane and the Sphere
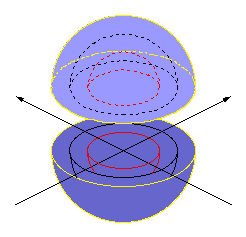
We will now generalize the line and circle to their higher-dimensional analogues: the plane and the sphere. The plane contains the original line and the sphere contains the original circle, so all the statements made earlier with respect to the interpretation of the circle and line carry over to the sphere and plane. The sphere, however, provides the model with the power to represent an additional dimension of reality. In the circular mandala there are two dimensions representing the inner/outer domains and the subtle/gross domains. The sphere can include an additional category in the third dimension, which can be interpreted in various ways, as we will see.
 To generalize from the circle and line to the higher-dimensional sphere and plane, extend from the center of the original circle (shown in red) a y-axis perpendicular to the plane of the circle (shown in yellow) and a corresponding unit circle (also shown in yellow). Thus, we have duplicated the original line and circle mandala (shown in red) along a second perpendicular direction. The points along the y-axis are identified with its circle just as the points along the x-axis are identified with its circle. More generally, any line in the x-y plane that passes through the origin will map to a corresponding circle, and just as all the lines through the origin sweep out a plane, all the corresponding circles sweep out a sphere. Viewing the sphere as a globe, these circles correspond to lines of longitude.
To generalize from the circle and line to the higher-dimensional sphere and plane, extend from the center of the original circle (shown in red) a y-axis perpendicular to the plane of the circle (shown in yellow) and a corresponding unit circle (also shown in yellow). Thus, we have duplicated the original line and circle mandala (shown in red) along a second perpendicular direction. The points along the y-axis are identified with its circle just as the points along the x-axis are identified with its circle. More generally, any line in the x-y plane that passes through the origin will map to a corresponding circle, and just as all the lines through the origin sweep out a plane, all the corresponding circles sweep out a sphere. Viewing the sphere as a globe, these circles correspond to lines of longitude.
The correspondence between points in the plane and points on the sphere is a natural generalization of the lower-dimensional case. Specifically, one imagines lines passing through the point at infinity located at the south pole of the sphere. Each of these lines intersects the plane at one point and intersects the sphere at one point, matching up the points in a one-to-one correspondence. For interested readers, mathematical details of this mapping between the sphere and the plane are described below in the mathematical appendix.
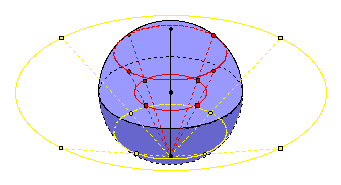 Since the line from the south to north pole intersects the plane at the origin, the north pole of the sphere is mapped to the origin of the plane. The south pole, however, is not mapped to a point in the plane. It corresponds to the point at infinity. Just as this point was discontinuously separated from the line in the lower-dimensional case, now it is also separated from the plane. From the perspective of the sphere, however, this point is part of the same unified continuum as all the other points. The points along the equator of the sphere map to the unit circle in the plane (which coincides with the equator since this is where the sphere intersects the plane). More generally, horizontal circles on the sphere (lines of latitude on the globe) map to concentric circles of various sizes in the plane. Note that circles of latitude in the northern hemisphere map to smaller circles in the plane, while circles of latitude in the southern hemisphere map to larger circles in the plane.
Since the line from the south to north pole intersects the plane at the origin, the north pole of the sphere is mapped to the origin of the plane. The south pole, however, is not mapped to a point in the plane. It corresponds to the point at infinity. Just as this point was discontinuously separated from the line in the lower-dimensional case, now it is also separated from the plane. From the perspective of the sphere, however, this point is part of the same unified continuum as all the other points. The points along the equator of the sphere map to the unit circle in the plane (which coincides with the equator since this is where the sphere intersects the plane). More generally, horizontal circles on the sphere (lines of latitude on the globe) map to concentric circles of various sizes in the plane. Note that circles of latitude in the northern hemisphere map to smaller circles in the plane, while circles of latitude in the southern hemisphere map to larger circles in the plane.
Symmetries of Hemispheres, Quadrants, and Levels
The points in the plane with positive values of x are mapped to the eastern hemisphere of the sphere, while the points with negative values of x are mapped to the western hemisphere. In other words, the y-z plane divides the sphere into two halves: one half that maps to a right half of the plane and another half that maps to the left half of the plane. These two halves of the plane are divided by the y-axis. Extending the interpretation given to the circle mandala, these halves correspond to the inner and outer domains of manifestation, with the y-axis representing the distinction between the two.
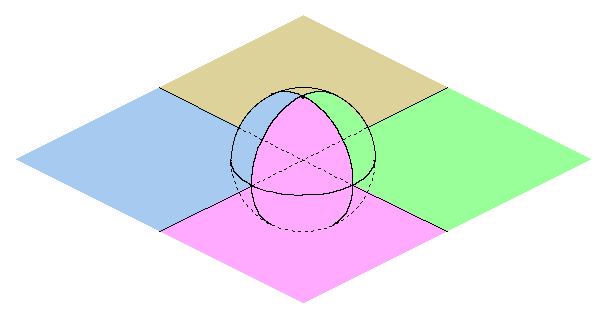 With an additional dimension, the plane also can be divided into points with positive values of y and points with negative values of y. These two halves of the plane are divided by the x-axis and correspond to the two hemispheres divided by the x-z plane. These two halves can be given various interpretations. For example, they can represent the distinction between singularity and plurality, manifesting in the world of objects the primordial distinction between One and Many. The two singular/plural hemispheres are orthogonal to the inner/outer hemispheres, dividing the sphere into four longitudinal regions, like sections of an orange. These regions map to four quadrants of the plane, representing the four possible combinations of the two divisions.
With an additional dimension, the plane also can be divided into points with positive values of y and points with negative values of y. These two halves of the plane are divided by the x-axis and correspond to the two hemispheres divided by the x-z plane. These two halves can be given various interpretations. For example, they can represent the distinction between singularity and plurality, manifesting in the world of objects the primordial distinction between One and Many. The two singular/plural hemispheres are orthogonal to the inner/outer hemispheres, dividing the sphere into four longitudinal regions, like sections of an orange. These regions map to four quadrants of the plane, representing the four possible combinations of the two divisions.
The reflection symmetry of the sphere that exchanges positive and negative values of x represents the interdependence of inner knowing and outer being, just as discussed earlier with the circle mandala. In addition, there is now a reflection symmetry of the sphere that exchanges positive and negative values of the new dimension y. This symmetry represents the interdependence and ultimate identity of singularity with plurality. The interdependence is illustrated by the fact that any plurality is composed of a collection of singulars, while any singular is part of a plurality. The x and y dimensions divide the plane orthogonally, generating four quadrants.
The points on the sphere in the upper hemisphere map to points in the plane that are contained within the unit circle, while the points in the lower hemisphere map to points in the plane that are outside the unit circle. The upper/lower distinction is interpreted as the distinction between gross and subtle, as discussed earlier in relation to the circle mandala. Points on the sphere that are closer to the north pole correspond to points in the plane that are closer to the origin, while points on the sphere that are closer to the south pole correspond to points in the plane that are further from the origin. Thus, the gradations of manifested objects correspond to the distance from the origin, so that the gross objects correspond to the northern hemisphere and the subtle objects correspond to the southern hemisphere.
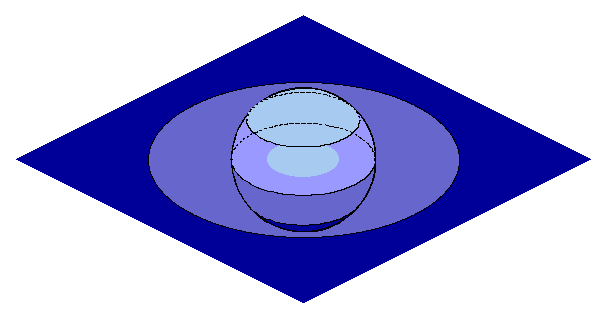 The sphere has a reflection symmetry that exchanges positive and negative values of z, reflecting points in the upper hemisphere to points in the lower hemisphere, and vice versa. This exchanges subtle and gross realms of manifestation, and the same interpretation discussed in relation to the circle mandala applies to the sphere as well: degrees of subtlety are mirrored by degrees of concreteness, with higher concreteness corresponding to higher subtlety. In the plane this reflection exchanges a point at a distance r from the origin with a point at a distance 1/r from the origin, thus exchanging large for small and vice versa. In particular, the most concrete point at the origin is exchanged with the point at infinity, symbolizing the identity of emptiness and form.
The sphere has a reflection symmetry that exchanges positive and negative values of z, reflecting points in the upper hemisphere to points in the lower hemisphere, and vice versa. This exchanges subtle and gross realms of manifestation, and the same interpretation discussed in relation to the circle mandala applies to the sphere as well: degrees of subtlety are mirrored by degrees of concreteness, with higher concreteness corresponding to higher subtlety. In the plane this reflection exchanges a point at a distance r from the origin with a point at a distance 1/r from the origin, thus exchanging large for small and vice versa. In particular, the most concrete point at the origin is exchanged with the point at infinity, symbolizing the identity of emptiness and form.
In contrast to the two longitudinal divisions of the sphere that split the plane into linear quadrants, the equatorial division of the sphere splits the plane into the inside and outside of a circle. While these divisions appear very different from the perspective of the plane, from the perspective of the sphere they are equivalent. All three divisions of the sphere split it into two hemispheres. This symmetry helps reveal that the various types of divisions in the plane are manifestations of a single type of division of the sphere. Put another way, we see that the same maxim "as above, so below" is at work in the different dimensions. Each dimension manifests a different aspect of the primordial One/Many distinction between the plane and the point at infinity. In the z-dimension this primordial distinction manifests its aspect of formlessness/form as the distinction subtle/gross. In the x-dimension it manifests its aspect of subjective/objective as the distinction inner/outer, and in the y-dimension it manifests its numerical aspect as the distinction singular/plural. The three dimensions can thus be seen as modes of representing different aspects of the primordial distinction of One/Many, unfolding its implicit meaning into explicit dimensions in different ways.
The symmetry of the sphere reveals not only insights due to reflection symmetries. The sphere also has a continuous rotation symmetry about any axis. Rotation about the y-axis represents the process of involution and evolution as it dynamically transforms through the dimensions of inner and outer. Rotation about the x-axis also represents the processes of involution and evolution, but now in relation to the dimensions of singular and plural. Rotation about the z-axis dynamically transforms the dimensions of inner/outer with those of singular/plural, leaving the evolutionary or involutionary level unchanged These rotational transformations are symbols for how reality is not fixed by our distinctions and categories, but dynamically flows through them, transforming them into each other.
It is interesting to note that the involutionary and evolutionary phases both have implicit and explicit aspects at each level. At the level of the transcendent, the One is explicit and the Many is implicit. At the level of the Gross, the Many is explicit and the One is implicit. The difference is that involution enfolds the implicit Many from the explicit One, while evolution unfolds the implicit One from the explicit Many. Both phases are needed to get a complete picture.
In the symmetry of the sphere, it is especially important to observe that the south pole is not a privileged point, but merely a point that was arbitrarily selected to create a frame of reference for describing the sphere and projecting it into a plane. Any point on the sphere could be selected. Thus any point on the sphere has equal potential to represent the point at infinity or a point in the plane. The sphere thus reveals as self-evident the ultimate identity of the transcendental subject with the manifest world of objects. More generally, the symmetry of the sphere reveals hidden relationships and dissolves paradoxes on the level of the plane. This mathematical mandala, therefore, serves not only as a symbol of reality, but also provides a tool for facilitating complex thinking (Morin, 1998), demonstrating how opposites exist in a dynamic co-implication.
It also can illustrate the coincidence of opposites, such as Nicholas of Cusa's identification of the line with the circle. In particular, some circles on the sphere (e.g., lines of longitude) map to lines in the plane, while other circles on the sphere (e.g., lines of latitude) map to circles in the plane. To be precise, a circle on the sphere maps to a line if the circle passes through the point at infinity, and it maps to a circle if it does not pass through the point at infinity. Whether a circle is appears in the plane as a line or a circle therefore depends simply on where the point at infinity is located. In other words, the sphere shows directly that the circle and the line are indeed identical, as Cusa argued more indirectly using the process of a circle growing larger and larger. We can even adapt Cusa's argument to the spherical mandala by rotating the equator around the x-axis through 90 degrees until it becomes a line of longitude. The image of this rotation in the sphere is a circle growing larger and larger until it becomes a line, exactly as Cusa argued. With the sphere, however, the identity of the two is always evident.
Alternative Divisions
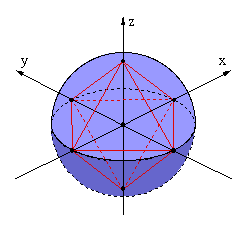 The spherical mandala suggests various alternative ways of dividing the sphere, resulting in many possible planar mandalas. The planar mandala with four quadrants and multiple levels arises by a particular symmetry-breaking of the sphere according to three coordinate axes. There are many other possible ways to break the symmetry of the sphere, however, and none is inherently privileged. For example, there are exactly five Platonic solids that break spherical symmetry in a way that corresponds to regular polyhedra. The octahedron with vertices aligned with the three axes naturally corresponds to the particular model we have illustrated above, with its eight faces corresponding to the eight regions of the sphere resulting from the equatorial division and the two longitudinal divisions. Its edges can be projected outward to the surface of the sphere, resulting in the two longitudinal divisions of the sphere and the equatorial division. These divisions are then projected as the x-axis and y-axis in the plane and the unit circle. Alternatively, one can discard the sphere and consider the mapping directly from the octahedron to the plane using the same map used for the sphere. Although this model retains all the reflection symmetries, it has the disadvantage that it no longer has the continuous rotational symmetry of the sphere.
The spherical mandala suggests various alternative ways of dividing the sphere, resulting in many possible planar mandalas. The planar mandala with four quadrants and multiple levels arises by a particular symmetry-breaking of the sphere according to three coordinate axes. There are many other possible ways to break the symmetry of the sphere, however, and none is inherently privileged. For example, there are exactly five Platonic solids that break spherical symmetry in a way that corresponds to regular polyhedra. The octahedron with vertices aligned with the three axes naturally corresponds to the particular model we have illustrated above, with its eight faces corresponding to the eight regions of the sphere resulting from the equatorial division and the two longitudinal divisions. Its edges can be projected outward to the surface of the sphere, resulting in the two longitudinal divisions of the sphere and the equatorial division. These divisions are then projected as the x-axis and y-axis in the plane and the unit circle. Alternatively, one can discard the sphere and consider the mapping directly from the octahedron to the plane using the same map used for the sphere. Although this model retains all the reflection symmetries, it has the disadvantage that it no longer has the continuous rotational symmetry of the sphere.
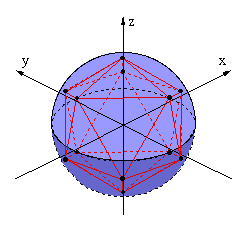 The other Platonic solids can also be inscribed in the sphere to produce other mandalas when projected into the plane. To give just one example, the icosahedron can be inscribed in the sphere to produce a planar mandala with five-fold symmetry. Its twenty faces map to twenty distinct regions in the plane, producing a particularly beautiful and complex mandala exhibiting a five-pointed star. There are also other ways to break the symmetry of the sphere that do not correspond to Platonic solids (i.e., discrete subgroups of the spherical group).
The other Platonic solids can also be inscribed in the sphere to produce other mandalas when projected into the plane. To give just one example, the icosahedron can be inscribed in the sphere to produce a planar mandala with five-fold symmetry. Its twenty faces map to twenty distinct regions in the plane, producing a particularly beautiful and complex mandala exhibiting a five-pointed star. There are also other ways to break the symmetry of the sphere that do not correspond to Platonic solids (i.e., discrete subgroups of the spherical group).
The spherical mandala, therefore, not only provides a higher-dimensional analogue for a particular four-quadrant planar mandala, but is the archetype for an infinite number of possible planar mandalas. These correspond to other possible models of the cosmos, different ways to draw distinctions among the manifest phenomena of reality. The sphere, like reality itself, does not dictate to us how it must be viewed or interpreted. It allows any number of modes of symmetry breaking to produce distinctions within itself and corresponding models when projected onto the plane. We may find that certain ways of making distinctions are more useful to us because they correspond more closely with our familiar ways of experiencing and thinking about the world. But the fundamental categories that provide structure to our experience are not ultimate. If we lose sight of this fact, then we lose sight of the sphere and fall into a planar model with one fixed set of distinctions. We have then lost our freedom to see reality from different perspectives.
Generalization to Arbitrary Dimensions
Although difficult to visualize or illustrate, the spherical mandala can be generalized to arbitrarily high dimensions. Just as the circle in two-dimensions has a one-to-one mapping to the one-dimensional line plus the point at infinity, and the sphere in three-dimensions has a mapping to the two-dimensional plane plus the point at infinity, so the "sphere" in four dimensions has a mapping to the three-dimensional space plus the point at infinity. Like the maps in the lower dimensional versions of the mandala, this map for the four-dimensional spherical mandala also uses lines through the point at infinity to match points on the four-dimensional sphere with points in three-dimensional space. The analog of circles of longitude in the three-dimensional spherical mandala are "spheres of longitude" on the four-dimensional spherical mandala. Just as circles of longitude in the three-dimensional spherical mandala map to lines in the plane, the spheres of longitude in the four-dimensional spherical mandala map to two-dimensional planes in three-dimensional space. Similarly, in much the same way that circles of latitude in the three-dimensional spherical mandala map to concentric circles in the plane, the "spheres of latitude" in the four-dimensional sphere map to concentric spheres in three-dimensional space.
The generalization of the spherical mandala to arbitrarily high dimensions allows the mandala to use additional dimensions to represent additional aspects of manifest reality. The circular mandala in two dimensions captures two aspects (inner/outer, subtle/gross), while the spherical mandala in three dimensions captures three aspects (inner/outer, subtle/gross, singular/plural). In general, to represent N distinct aspects of each object, a sphere of N dimensions is used.
The symmetries of the spherical mandala then illustrate the dynamic transformations and relationships between these N aspects. Mathematical details of this generalization are contained in the mathematical appendix for the interested reader.
Relation to Ken Wilber's Model
Readers familiar with the work of Ken Wilber will no doubt have noticed already that the planar mandala discussed above has many features in common with his all-quadrant, all-level (AQAL) model of the Kosmos (Wilber, 1996, 1998). In both cases, the plane is divided into four quadrants by the vertical and horizontal axes which represent the inner/outer and singular/plural distinctions. In addition, both planes have levels radiating outward from the center that represent the subtle/gross dimension. These correspondences are not entirely accidental. The mandala of the circle and line presented in the first section of this paper above was developed by the author independently of the AQAL model. However, when the mandala was generalized to higher dimensions, it became evident to the author that the added dimension could be interpreted so that the planar projection of the sphere would generate a mandala very similar to the AQAL model. The spherical mandala presented in this paper, in other words, has as one of its instances a planar projection that exhibits many of the properties of the AQAL model.
 There are, however, some noticeable differences between the models. First of all, the AQAL planar mandala is not presented as mathematically equivalent to a single higher-dimensional sphere. The AQAL model is, however, sometimes described as a collection of concentric nested spheres, with the planar AQAL representation being a cross-section of this collection of nested spheres. Each concentric circle in the planar representation corresponds to an equator of a different concentric sphere. In contrast, in the integral sphere model, the nested circles in the plane do not correspond to equators of multiple nested spheres, but to lines of latitude on a single sphere, thus integrating them all. More generally, in the integral sphere mandala, a single sphere simultaneously encodes all levels and all quadrants in the plane, whereas the AQAL model requires multiple spheres. It should be noted that a single four-dimensional integral sphere maps to a three-dimensional space of infinitely nested concentric spheres (corresponding to "spheres of latitude" on the four-dimensional integral sphere). Wilber's nested spheres, therefore, can be seen as a special case of the spherical mandala as well.
There are, however, some noticeable differences between the models. First of all, the AQAL planar mandala is not presented as mathematically equivalent to a single higher-dimensional sphere. The AQAL model is, however, sometimes described as a collection of concentric nested spheres, with the planar AQAL representation being a cross-section of this collection of nested spheres. Each concentric circle in the planar representation corresponds to an equator of a different concentric sphere. In contrast, in the integral sphere model, the nested circles in the plane do not correspond to equators of multiple nested spheres, but to lines of latitude on a single sphere, thus integrating them all. More generally, in the integral sphere mandala, a single sphere simultaneously encodes all levels and all quadrants in the plane, whereas the AQAL model requires multiple spheres. It should be noted that a single four-dimensional integral sphere maps to a three-dimensional space of infinitely nested concentric spheres (corresponding to "spheres of latitude" on the four-dimensional integral sphere). Wilber's nested spheres, therefore, can be seen as a special case of the spherical mandala as well.
 Another significant difference is that the AQAL mandala does not have a point at infinity that transcends the plane (or that transcends the nested spheres). Although Wilber refers to the entire space of the plane as symbolizing an omnipresence or immanence throughout all levels and quadrants, this is not equivalent to a point at infinity which transcends and is distinct from the plane. In the spherical mandala, the point at infinity is an explicit element of the model and provides insight into the relationship between transcendent and manifest orders. The omnipresence is represented in the spherical mandala through the symmetry of the sphere that demonstrates the equivalence of the point at infinity with all other points on the sphere.
Another significant difference is that the AQAL mandala does not have a point at infinity that transcends the plane (or that transcends the nested spheres). Although Wilber refers to the entire space of the plane as symbolizing an omnipresence or immanence throughout all levels and quadrants, this is not equivalent to a point at infinity which transcends and is distinct from the plane. In the spherical mandala, the point at infinity is an explicit element of the model and provides insight into the relationship between transcendent and manifest orders. The omnipresence is represented in the spherical mandala through the symmetry of the sphere that demonstrates the equivalence of the point at infinity with all other points on the sphere.
One might also note that the integral sphere has the virtue that it can be generalized to arbitrarily high dimensions, and thus represent more than just the three dimensions of the AQAL mandala. This could be particularly useful as a way to include in the mandala additional dimensions of holons that Wilber discusses but does not explicitly represent in the mandala.
The Integral Sphere and Integral Science
The spherical mandala can provide the context for a profound vision of integral science, i.e., a knowing that is comprehensive of all levels and aspects of reality. As we have just seen with the transformation between evolutionary and involutionary models, the spherical mandala can represent and relate different planar mandalas. Through symmetry transformations of the sphere the mandala can reveal hidden aspects of a planar mandala and transform it into related mandalas. This property is a powerful tool of understanding. The spherical mandala can also relate and integrate apparently different parts of a planar mandala from a higher-dimensional perspective. When applied to the discipline of deepening our knowledge of reality (i.e., science), the spherical mandala provides fertile ground for unfolding many insights that open up and reveal depths and relationships that would remain hidden within the context of a single planar model.
Like the AQAL model, the spherical mandala encourages us to include all the levels and quadrants. For example, integral science is not just limited to the true, but must also include the good and the beautiful. Without the ethical canons of scientific community, scientists could lie and falsify data. Since there would be no trust of other scientific reports or data, the entire scientific enterprise would collapse. Beauty also is an integral part of science insofar as it influences the selection of theories based on aesthetic criteria. And, of course, the passion for truth provides the fundamental motive for scientific inquiry. A fully integral science includes all these values more explicitly. It also includes the good through the recognition that scientific theories influence cultural worldviews as much as worldviews influence science. Moreover, an integral science must acknowledge the valid aspects of the constructivist critiques, maintain self-awareness of its social and cultural influences and biases, and take responsibility for them.
For an integral science to incorporate all levels means that it employs not only the physical organs of sensory knowledge, but also the conceptual and higher levels of knowing as well. When applied to the physical domain, science requires use of our sensory modes of knowledge to access data about physical objects. In addition, science is not mere observation. It necessarily involves abstract conceptual representation when formulating theories and deriving consequence from them. And, insofar as integral science takes subtle objects as its domain of study (such as in sacred sciences), it will also require the exercise of subtle organs of knowledge. An integral science, however, does not simply mean that these aspects are all included. It means they are integrated and seen as interdependent and ultimately inseparable. The symmetry of the integral sphere illustrates this truth in a way that no planar model can do. For example, the fact that all data is theory-laden illustrates the implicit dependence of sensory knowledge on theoretical knowledge. All our scientific knowledge implicitly involves conceptual knowledge, even at the level of the "raw facts." Similarly, conceptual knowledge and sensory knowledge both implicitly presuppose the primordial capacity to be aware. These subtle interdependencies between the levels are easy to overlook in a static planar model. Moreover, the reflection symmetries of the spherical mandala help us remember that the deepening of our knowledge of nature is not a simple matter of simply looking, but a process of interactive dialogue with nature in which we pose questions in the form of controlled experiments, receive responses in the form of data, attempt to understand what we are being told through a process of interpretation using theories, and then pose new questions to refine our understanding. In the spherical model, the symmetry transformations dynamically transform and relate both the levels and quadrants, providing a symbolic representation of these deep interdependencies and helping guard against an oversimplification of epistemological realities.
The spherical mandala, by including the point at infinity, helps us remember that the planar world of manifest forms is not ultimate. Thus, any form or structure within the planar mandala is conditioned and limited in its scope. For example, the scientific method itself, even when generalized to its most essential features, has limitations. In particular, the methods of arriving at valid knowledge no longer apply when approaching the point at infinity. There, the distinctions between interior/exterior, individual/collective, and knowing/being no longer apply. As all the mystics have testified, nondual realization, at its own level, is not the result of following an injunction, is not an object of knowledge apart from the subject of awareness, allows for no distinction between true and false, and does not depend upon communal validation for its authority. In other words, it transcends the scientific method. Thus, we should view this method as applicable only to the levels at which it is meaningful to talk of injunctions and confirmations of an individual and a community in dialogue. An integral science should acknowledge these limitations, and view the scientific method as a technique useful at most levels for helping individuals in a community develop a body of shared knowledge. Science, in other words, is itself a stage in our collective deepening of our communion with reality. We can thus practice integral science as a spiritual path, remembering that the scientific method is but a raft to help us cross the shore of lower levels. Once we reach the proximity of the infinite, it must left behind or else it becomes a barrier rather than a vehicle. If we cling to the structures of the plane, we will never realize the integral sphere in all its symmetric glory.
Finally, an integral science is not limited to the domain of gross exteriors, but includes within its potential domains of study the subtler realities as well. Integral science includes both the integral study of the physical plane of matter and the integral study of the subtle levels of reality. The potentials of integral science include not only a science of the physical correlates of subtle exteriors at the level of gross exteriors, but the subtle exteriors themselves, directly on their own terms. Even more profoundly, the integral sphere reminds us that the levels of reality interpenetrate each other and are not mutually exclusive. Each level is implicitly present in the others. Integral science is thus much more than simply viewing the subtle and gross realities as separate domains that should both be included. Rather, the symmetry of the integral sphere reminds us that the different depths of reality are simultaneously present in each object, regardless of which level appears explicit and which level appears implicit. By shifting our point of view in the higher-dimensional sphere, we can see how subtle is gross and gross is subtle, and how emptiness is form and form is emptiness.
The integral sphere therefore provides a higher-dimensional perspective relating and ultimately uniting aspects and levels of planar mandalas, honoring of a holistic diversity of presence in manifest without losing continuity with the unmanifest. Although science operating from the perspective of manifest diversity and flux seeks to discern unity and invariance, true integral science does not discard the one and reduce reality to the other, but acknowledges and integrates all levels, including the point at infinity that is ultimately seen to be already omnipresent.
Mathematical Appendix
 The extended real numbers R*=R∪{∞}
consists of the regular set of real numbers and a special point called the point at infinity, denoted ∞. The extended real numbers can be put into one-to-one correspondence with the points of the unit circle
S1 = {(x,z)∈R2 : x2+z2=1}
using the map
φ:S1→R* given by (x,z)→x/(1+z) and (0,−1)→∞. The inverse map φ−1:R*→S1 is given by s→(2s,1−s2)/(1+s2) and ∞→(0,−1).
The extended real numbers R*=R∪{∞}
consists of the regular set of real numbers and a special point called the point at infinity, denoted ∞. The extended real numbers can be put into one-to-one correspondence with the points of the unit circle
S1 = {(x,z)∈R2 : x2+z2=1}
using the map
φ:S1→R* given by (x,z)→x/(1+z) and (0,−1)→∞. The inverse map φ−1:R*→S1 is given by s→(2s,1−s2)/(1+s2) and ∞→(0,−1).
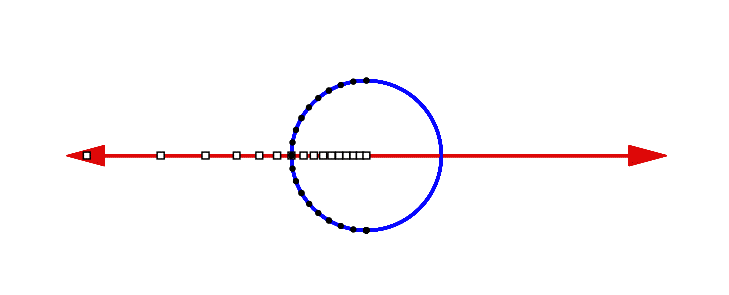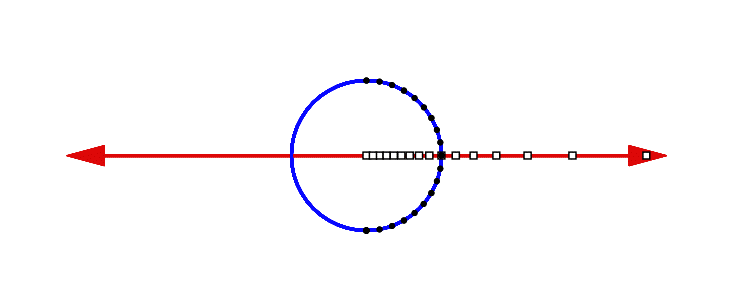
 This map can be visualized by drawing lines radiating out from the point (0,−1). Each line intersects the real number line at one point and intersects the circle at one point, forming a one-to-one correspondence between them. This set of lines is the projective space P1, where the horizontal line through (0,−1) which does not intersect the line corresponds to the point at infinity ∞. Another way to visualize the map is to imagine cutting the circle at its bottom, then pulling the two endpoints apart to straighten the circle into a line segment, then stretching the line segment to extend the two end points outward infinitely far.
This map can be visualized by drawing lines radiating out from the point (0,−1). Each line intersects the real number line at one point and intersects the circle at one point, forming a one-to-one correspondence between them. This set of lines is the projective space P1, where the horizontal line through (0,−1) which does not intersect the line corresponds to the point at infinity ∞. Another way to visualize the map is to imagine cutting the circle at its bottom, then pulling the two endpoints apart to straighten the circle into a line segment, then stretching the line segment to extend the two end points outward infinitely far.
The following theorems demonstrate that there is a remarkable correspondence between geometrical transformations of the circle and algebraic transformations in the real number line.
Theorem 1.
 The additive inverse in R corresponds to reflection through the z-axis in S1, and the multiplicative inverse in R corresponds to reflection through the x-axis in S1. Moreover, the antipode corresponds to the additive inverse of the multiplicative inverse.
The additive inverse in R corresponds to reflection through the z-axis in S1, and the multiplicative inverse in R corresponds to reflection through the x-axis in S1. Moreover, the antipode corresponds to the additive inverse of the multiplicative inverse.
Proof.
Let (x,z)∈S1 and let s=φ(x,z) be the corresponding point in R. The reflection of (x,z) about the z-axis is (−x,z) and the corresponding point in R is φ(−x,z). Now by definition φ(−x,z) + φ(x,z) = −x/(1+z) + x/(1+z) = (−x+x)/(1+z) = 0/(1+z) = 0. Thus φ(−x,z) = −φ(x,z) = −s.
 Similarly, the reflection of (x,z) about the x-axis is (x,−z) and the corresponding point in R is φ(x,−z). Now by definition φ(x,−z)φ(x,z) = [x/(1−z)][x/(1+z)] = x2/(1−z2) = x2/x2 = 1. Thus φ(−x,z) = 1/φ(x,z) = 1/s.
Similarly, the reflection of (x,z) about the x-axis is (x,−z) and the corresponding point in R is φ(x,−z). Now by definition φ(x,−z)φ(x,z) = [x/(1−z)][x/(1+z)] = x2/(1−z2) = x2/x2 = 1. Thus φ(−x,z) = 1/φ(x,z) = 1/s.
Finally, observe that the antipode of a point (x,z) is the point (−x,−z) obtained by reflection through both the x-axis and the z-axis in S1. Thus, by combining the above results, the antipode is the composition of the additive and multiplicative inverses. ♦
Corollary.
Let Rx be reflection through the x-axis, Rz be reflection through the z-axis, and s be a point in R. Then φ(Rx(φ−1(ex)))=eφ(Rz(φ−1(x))). In other words, Reflection through the x-axis after exponentiation is equivalent to reflection through the z-axis before exponentiation. This is a result of the fact that exponentiation maps addition to multiplication. Thus, an inverse in the additive domain (Rz) before exponentiation is mapped to an inverse in the multiplicative domain (Rx) after exponentiation.
It is interesting to note that the points on the unit circle may be described by S1 = {eiθ : 0≤θ≤2π}. In particular, we can map a point (x,z) to the point z+ix = cosθ+isinθ = eiθ. Then, a rotation of 180 degrees (π radians) from (0,1) to the point at infinity (0,−1) corresponds to the identity eiπ=−1. This mysterious identity is thus a mathematical symbol for the turning about of the light of consciousness toward its source (Wolff, 1995).
 We can extend this correspondence between linear and circular space to a higher dimension as follows.
The extended complex numbers C*=C∪{∞}
can be put into one-to-one correspondence with the points of the sphere
S2 = {(x,y,z)∈R3 : x2+y2+z2=1}
using the map
φ: S2→C* given by (x,y,z)→(x+iy)/(1+z) and (0,0,−1)→∞. The inverse map φ−1: C*→S2 is given by w→(w†+w,w†−w,1−w†w)/(1+w†w) and ∞→(0,0,−1), where the complex conjugate of w is denoted here by w†.
We can extend this correspondence between linear and circular space to a higher dimension as follows.
The extended complex numbers C*=C∪{∞}
can be put into one-to-one correspondence with the points of the sphere
S2 = {(x,y,z)∈R3 : x2+y2+z2=1}
using the map
φ: S2→C* given by (x,y,z)→(x+iy)/(1+z) and (0,0,−1)→∞. The inverse map φ−1: C*→S2 is given by w→(w†+w,w†−w,1−w†w)/(1+w†w) and ∞→(0,0,−1), where the complex conjugate of w is denoted here by w†.
This map can be visualized by drawing lines from the south pole of the sphere. Each line will intersect the sphere in one point and will intersect the x-y plane in one point, forming the correspondence. The points on the x-axis map to a unit circle (shown in red), just as in the lower-dimensional case.
Similarly, the points on the y-axis map to another unit circle (shown in yellow). This map can also be visualized by imagining that the sphere is punctured at the south pole and stretched out so that the surface is flattened, similar to how the circle is cut at the bottom and stretched out.
Theorem 2.
The additive inverse in C corresponds to reflection in S2 through the x-z and y-z planes, and the multiplicative inverse in C corresponds to reflection in S2 through the x-y and x-z planes. Moreover, the antipode in S2 corresponds to the additive inverse of the multiplicative inverse of the complex conjugate.
Proof.
 Let (x,y,z)∈S2 and let w=φ(x,y,z) be the corresponding point in C. The reflection of (x,y,z) through both the x-z and y-z planes is the point (−x,−y,z) and the corresponding point in C is φ(−x,−y, z). Now by definition φ(−x,−y,z) + φ(x,y,z) = (−x−iy)/(1+z) + (x+iy)/(1+z) = 0/(1+z) = 0. Thus φ(−x,−y,z) = −φ(x,y,z) = −w.
Let (x,y,z)∈S2 and let w=φ(x,y,z) be the corresponding point in C. The reflection of (x,y,z) through both the x-z and y-z planes is the point (−x,−y,z) and the corresponding point in C is φ(−x,−y, z). Now by definition φ(−x,−y,z) + φ(x,y,z) = (−x−iy)/(1+z) + (x+iy)/(1+z) = 0/(1+z) = 0. Thus φ(−x,−y,z) = −φ(x,y,z) = −w.
Similarly, the reflection of (x,y,z) through the x-y and x-z planes is (x,−y,−z) and the corresponding point in C is φ(x,−y,−z). Now by definition φ(x,−y,−z)φ(x,y,z) = [(x−iy)/(1−z)][(x+iy)/(1+z)] = (x2+y2)/(1−z2) = 1. Thus φ(x,−y,−z) = 1/φ(x,y,z) = 1/w.
Furthermore, the antipode of a point (x,y,z) is the reflection of (x,y,z) through the x-y, x-z, and y-z planes to give (−x,−y,−z). Combining the previous results, the composition of the additive and multiplicative inverses corresponds to reflection through the x-y and y-z planes, taking (x,y,z) to (−x,y,−z). Now observe that complex conjugation of a number w∈C to obtain w* corresponds to reflection through the x-z plane, taking (x,y,z) to (x,−y,z). Indeed, φ(x,y,z)* = (x+iy)*/(1+z) = (x−iy)/(1+z) = φ(x,−y,z). Thus, combining complex conjugation with the additive and multiplicative inverses to obtain −1/w* corresponds to taking a point (x,y,z) to its antipode (−x,−y,−z).
♦
It is interesting to note that circles on the sphere map to circles or lines in the plane. In particular, circles passing through the south pole map to lines in the plane, while all other circles map to circles in the plane. Thus, while lines and circles are distinguished in the plane, they are indistinguishable on the sphere.
Instead of identifying the plane with the complex numbers, it can be simply treated as the regular Euclidean plane without any additional structure. In this case, the sphere S2 = {(x,y,z)∈R3 : x2+y2+z2=1} is mapped to the extended Euclidean plane R2*=R2∪{∞} with the map φ:S2→R2* given by (x,y,z)→(x/(1+z),y/(1+z)) and (0,0,−1)→∞. More generally, the n-sphere Sn = {(x0,...,xn)∈Rn : x02+...+xn2=1} can be mapped to the extended Euclidean n-dimensional space Rn*=Rn∪{∞} with the map
φ:Sn→Rn* given by (x0,...,xn)→((x1/(1+x0),...,(xn/(1+x0)) and (−1,0,...,0)→∞. In the case of n=3 it is relevant to note that S3 can be identified with the unit quaternions SH={a+bi+cj+dk : a2+b2+c2+d2=1}. Therefore, extended Euclidean three-dimensional space R3* can be given an arithmetic structure. Then similar properties can be investigated as was done above with the complex numbers, relating geometric transformations in S3 and R3* to algebraic transformations in the unit quaterions SH. There is an even richer level of structure to investigate here since the algebraic structure of SH makes S3 into a Lie group. Moreover, SH is Lie isomorphic to SU(2), where SU(2)={A∈Mat(2,C) : A†A=I, det(A)=1}. (Note: SU(2) is the weak isospin internal symmetry of the standary model of elementary particles. It is also the double cover of SO(3) which is the group of rotations in R3.) The interpretation within the spherical mandala of these algebraic structures is a topic of further investigation.
Bibliography
Bohm, David and Peat, F. David (1987). Science, order, and creativity (Toronto ; New York : Bantam Books).
Burtt, E. A. (1955). The Metaphysical Foundations of Modern Physical Science (Garden City, NY: Doubleday).
Nicholas of Cusa (1997), Nicholas of Cusa: Selected Spiritual Writings, H. Lawrence Bond, tr., (New York: Paulist Press).
Lovejoy, Arthur O. (1973). The Great Chain of Being (Cambridge : Harvard University Press).
Merrell-Wolff, Franklin (1994). Franklin Merrell-Wolff's Experience and Philosophy (Albany : State University of New York Press).
Merrell-Wolff, Franklin (1995). Transformations in consciousness : the metaphysics and epistemology : containing his Introceptualism (Albany : State University of New York Press).
Morin, Edgar and Kern, Anne Brigitte (1998). Homeland earth : a manifesto for the new millennium (Cresskill, N.J. : Hampton Press).
Smith, Huston (1976). Forgotten Truth: The Primordial Tradition (New York : Harper Colophon).
von Franz, Marie-Louise (1974), Number and Time: Reflections Leading toward a Unification of Depth Psychology and Physics, (Evanston: Northwestern University Press).
Wallace, B. Alan (1996). Choosing reality : a Buddhist view of physics and the mind (Ithaca, N.Y. : Snow Lion Publications).
Wilber, Ken (1990). Eye to eye : the quest for the new paradigm (Boston : Shambhala).
Wilber, Ken (1996). A brief history of everything (Boston : Shambhala).
Wilber, Ken (1998). The marriage of sense and soul : integrating science and religion (New York : Random House).
Argüelles, José and Miriam (1972). Mandala (Berkeley: Shambhala).
Parmenides (1987). Early Greek Philosophy Jonathan Barnes, tr. (New York: Penguin).
Plotinus (1991). Plotinus: The Enneads, Stephen MacKenna, tr. (New York: Penguin).
Proclus (1987). Proclus' Commentary on Plato's Parmenides, G. R. Morrow and J. M.
Dillon, tr. (Princeton: Princeton University Press).
Cusa, Nicholas of (1997). Nicholas of Cusa: Selected Spiritual Writings, H. Lawrence Bond, tr. (New York: Paulist Press).
Ahlfors, Lars V. (1979). Complex Analysis (New York: McGraw-Hill).
Plato (1963). The Collected Dialogues of Plato, E. Hamilton and H. Cairns, eds. (Princeton: Princeton University Press).
Norbu, Chögyal Namkhai and Clemente, Adriano (1999). The Supreme Source: The Kunjed Gyalpo, The Fundamental Tantra of Dzogchen Semde (Ithaca: Snow Lion).
Whitehead, A. N. (1985). Process and Reality (New York: The Free Press).
Singer, I. M. and Thorpe, J. A. (1967). Lecture Notes on Elementary Topology and Geometry (New York: Springer-Verlag).
Smith, Huston (1977). Forgotten Truth: The Primordial Tradition (New York: Harper Colophon).
Shankara (1978). Shankara's Crest-Jewel of Discrimination, Swami Prabhavananda and C. Isherwood, tr. (Hollywood: Vedanta Press).
 In nearly every culture, mandalas have been used as symbolic representations of reality (Argüelles, 1972; see also Cunningham's Mandala Project). Typically, a mandala contains symbolic icons which have special meaning, and these symbols are arranged to show their places in the cosmos. Some mandalas, such as the sri yantra, contain geometric rather than iconic symbols and the spatial relationships between these geometric symbols carry the primary symbolic meaning. In addition to representing the cosmos in a compact, symbolic form, mandalas are used as tools for contemplation and inner transformation. Meditation upon a mandala, for example, can reveal deeper relationships between various parts of reality and help one to attain a more integral vision of oneself and the cosmos.
In nearly every culture, mandalas have been used as symbolic representations of reality (Argüelles, 1972; see also Cunningham's Mandala Project). Typically, a mandala contains symbolic icons which have special meaning, and these symbols are arranged to show their places in the cosmos. Some mandalas, such as the sri yantra, contain geometric rather than iconic symbols and the spatial relationships between these geometric symbols carry the primary symbolic meaning. In addition to representing the cosmos in a compact, symbolic form, mandalas are used as tools for contemplation and inner transformation. Meditation upon a mandala, for example, can reveal deeper relationships between various parts of reality and help one to attain a more integral vision of oneself and the cosmos.
 Notice that there is a discontinuity between the manifest line and the unmanifest point at infinity. No movement along the line, no matter how far out, will ever reach the transcendent point. Conversely, the transcendent point can never appear among the objects of the world. To illustrate this mathematically, a point on the line can be called the origin, and the line can be given a metric so that one can measure distances from the origin. The line then becomes a number line, such as the real number line, where each point corresponds to a number. The origin corresponds to zero, points to the right of the origin correspond to the positive numbers, and points to the left of the origin correspond to negative numbers. Points further and further from the origin correspond to larger and larger numbers. No matter how far away the point, though, it will always correspond to some finite number. Just as infinity is not a finite number, the point at infinity is not a point on the line. It transcends the points on the line, just as infinity transcends all finite numbers.
Notice that there is a discontinuity between the manifest line and the unmanifest point at infinity. No movement along the line, no matter how far out, will ever reach the transcendent point. Conversely, the transcendent point can never appear among the objects of the world. To illustrate this mathematically, a point on the line can be called the origin, and the line can be given a metric so that one can measure distances from the origin. The line then becomes a number line, such as the real number line, where each point corresponds to a number. The origin corresponds to zero, points to the right of the origin correspond to the positive numbers, and points to the left of the origin correspond to negative numbers. Points further and further from the origin correspond to larger and larger numbers. No matter how far away the point, though, it will always correspond to some finite number. Just as infinity is not a finite number, the point at infinity is not a point on the line. It transcends the points on the line, just as infinity transcends all finite numbers.
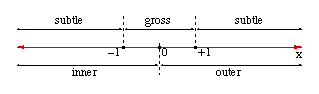 This grading of the points on the line separates them naturally into those near the origin with small values, and those far away from the origin with large values. For example, those points between −1 and +1 can be called gross phenomena or concrete objects. They do not enjoy much invariance and are thus least real and valuable. Those points to the left of −1 and to the right of +1 can be called the subtle phenomena or formal objects. They have high invariance, value, and reality. Note that this distinction between subtle and gross within the realm of objects reflects the primordial distinction between the infinite and the finite. This mirroring of the One/Many distinction in the world of form as the Large/Small distinction is a symbolic representation of the principle "as above, so below" which generates levels of order among phenomena.
This grading of the points on the line separates them naturally into those near the origin with small values, and those far away from the origin with large values. For example, those points between −1 and +1 can be called gross phenomena or concrete objects. They do not enjoy much invariance and are thus least real and valuable. Those points to the left of −1 and to the right of +1 can be called the subtle phenomena or formal objects. They have high invariance, value, and reality. Note that this distinction between subtle and gross within the realm of objects reflects the primordial distinction between the infinite and the finite. This mirroring of the One/Many distinction in the world of form as the Large/Small distinction is a symbolic representation of the principle "as above, so below" which generates levels of order among phenomena.

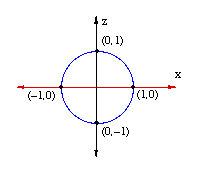 We begin by drawing a vertical z-axis through the line to form a Cartesian coordinate system with the origin of the x-axis at (0,0) and the point at infinity at (0,−1).
Now draw a circle of radius 1 with its center at the origin. Note that the point at infinity corresponds to the bottom point on the circle. In addition, the points (−1,0) and (1,0) on the line correspond to points on the circle. There is thus a self-evident correspondence between three points on the circle and three points of the linear mandala. Moreover, there is a one-to-one correspondence between all the other points on the line and all the other points on the circle. To see this correspondence, imagine a line rotating around the pivot point (0,-1) or, if you prefer, an infinite number of lines radiating outward from (0,-1), the point at infinity. Each of these lines intersects the x-axis at a single point and also intersects the circle at a single point. In other words, each line creates a one-to-one correspondence between a point on the line and a point on the circle. This means that the circle is equivalent to the line.
We begin by drawing a vertical z-axis through the line to form a Cartesian coordinate system with the origin of the x-axis at (0,0) and the point at infinity at (0,−1).
Now draw a circle of radius 1 with its center at the origin. Note that the point at infinity corresponds to the bottom point on the circle. In addition, the points (−1,0) and (1,0) on the line correspond to points on the circle. There is thus a self-evident correspondence between three points on the circle and three points of the linear mandala. Moreover, there is a one-to-one correspondence between all the other points on the line and all the other points on the circle. To see this correspondence, imagine a line rotating around the pivot point (0,-1) or, if you prefer, an infinite number of lines radiating outward from (0,-1), the point at infinity. Each of these lines intersects the x-axis at a single point and also intersects the circle at a single point. In other words, each line creates a one-to-one correspondence between a point on the line and a point on the circle. This means that the circle is equivalent to the line.

 Even deeper yet, we can recognize that the circle has perfect symmetry of all its points: there is no intrinsic difference between the points. No point is inherently privileged or distinguished. Consequently, we are free to select any point as the transcendent subject, or point at infinity. While the linear mandala is fixed to a particular subjective point, the circular mandala invites free transformation, allowing any point on the circle to be regarded as the point from which the manifest world of objects is projected. From the perspective of the circle, it is evident that every point is potentially both a transcendent subject and a manifest object, both emptiness and form. Or, put another way, the transcendent subject is omnipresent and immanent in every object. Prior to the selection of a point at infinity, all points are equally subjective and objective. Moreover, any given point can simultaneously be a subject to which a particular manifest world appears, and an object within the manifest world appearing relative to another subjective point. But, insofar as all the points of the circle are indistinguishable, these subjects are identical. The circle is One continuous unity.
Even deeper yet, we can recognize that the circle has perfect symmetry of all its points: there is no intrinsic difference between the points. No point is inherently privileged or distinguished. Consequently, we are free to select any point as the transcendent subject, or point at infinity. While the linear mandala is fixed to a particular subjective point, the circular mandala invites free transformation, allowing any point on the circle to be regarded as the point from which the manifest world of objects is projected. From the perspective of the circle, it is evident that every point is potentially both a transcendent subject and a manifest object, both emptiness and form. Or, put another way, the transcendent subject is omnipresent and immanent in every object. Prior to the selection of a point at infinity, all points are equally subjective and objective. Moreover, any given point can simultaneously be a subject to which a particular manifest world appears, and an object within the manifest world appearing relative to another subjective point. But, insofar as all the points of the circle are indistinguishable, these subjects are identical. The circle is One continuous unity.
 The correspondence between the line and the circle maps the negative valued points on the left side of the line to the left half of the circle and maps the positive valued points on the right side of the line to the right half of the circle. These two halves of the circle correspond to the inner and outer objects of the manifest world. What is less obvious is that the correspondence maps the small valued points near the origin to the upper half of the circle and maps the large valued points to the lower half of the circle. These two halves of the circle correspond to the gross and subtle objects. It is remarkable that while the subtle/gross distinction and the inner/outer distinction appear very differently in the linear mandala, in the circular mandala they have identical form, i.e., both these primordial distinctions arise from the simple act of dividing the world of objects into two halves, the only difference being whether the dividing line is vertical or horizontal.
The correspondence between the line and the circle maps the negative valued points on the left side of the line to the left half of the circle and maps the positive valued points on the right side of the line to the right half of the circle. These two halves of the circle correspond to the inner and outer objects of the manifest world. What is less obvious is that the correspondence maps the small valued points near the origin to the upper half of the circle and maps the large valued points to the lower half of the circle. These two halves of the circle correspond to the gross and subtle objects. It is remarkable that while the subtle/gross distinction and the inner/outer distinction appear very differently in the linear mandala, in the circular mandala they have identical form, i.e., both these primordial distinctions arise from the simple act of dividing the world of objects into two halves, the only difference being whether the dividing line is vertical or horizontal.
 To generalize from the circle and line to the higher-dimensional sphere and plane, extend from the center of the original circle (shown in red) a y-axis perpendicular to the plane of the circle (shown in yellow) and a corresponding unit circle (also shown in yellow). Thus, we have duplicated the original line and circle mandala (shown in red) along a second perpendicular direction. The points along the y-axis are identified with its circle just as the points along the x-axis are identified with its circle. More generally, any line in the x-y plane that passes through the origin will map to a corresponding circle, and just as all the lines through the origin sweep out a plane, all the corresponding circles sweep out a sphere. Viewing the sphere as a globe, these circles correspond to lines of longitude.
To generalize from the circle and line to the higher-dimensional sphere and plane, extend from the center of the original circle (shown in red) a y-axis perpendicular to the plane of the circle (shown in yellow) and a corresponding unit circle (also shown in yellow). Thus, we have duplicated the original line and circle mandala (shown in red) along a second perpendicular direction. The points along the y-axis are identified with its circle just as the points along the x-axis are identified with its circle. More generally, any line in the x-y plane that passes through the origin will map to a corresponding circle, and just as all the lines through the origin sweep out a plane, all the corresponding circles sweep out a sphere. Viewing the sphere as a globe, these circles correspond to lines of longitude.
 Since the line from the south to north pole intersects the plane at the origin, the north pole of the sphere is mapped to the origin of the plane. The south pole, however, is not mapped to a point in the plane. It corresponds to the point at infinity. Just as this point was discontinuously separated from the line in the lower-dimensional case, now it is also separated from the plane. From the perspective of the sphere, however, this point is part of the same unified continuum as all the other points. The points along the equator of the sphere map to the unit circle in the plane (which coincides with the equator since this is where the sphere intersects the plane). More generally, horizontal circles on the sphere (lines of latitude on the globe) map to concentric circles of various sizes in the plane. Note that circles of latitude in the northern hemisphere map to smaller circles in the plane, while circles of latitude in the southern hemisphere map to larger circles in the plane.
Since the line from the south to north pole intersects the plane at the origin, the north pole of the sphere is mapped to the origin of the plane. The south pole, however, is not mapped to a point in the plane. It corresponds to the point at infinity. Just as this point was discontinuously separated from the line in the lower-dimensional case, now it is also separated from the plane. From the perspective of the sphere, however, this point is part of the same unified continuum as all the other points. The points along the equator of the sphere map to the unit circle in the plane (which coincides with the equator since this is where the sphere intersects the plane). More generally, horizontal circles on the sphere (lines of latitude on the globe) map to concentric circles of various sizes in the plane. Note that circles of latitude in the northern hemisphere map to smaller circles in the plane, while circles of latitude in the southern hemisphere map to larger circles in the plane.
 With an additional dimension, the plane also can be divided into points with positive values of y and points with negative values of y. These two halves of the plane are divided by the x-axis and correspond to the two hemispheres divided by the x-z plane. These two halves can be given various interpretations. For example, they can represent the distinction between singularity and plurality, manifesting in the world of objects the primordial distinction between One and Many. The two singular/plural hemispheres are orthogonal to the inner/outer hemispheres, dividing the sphere into four longitudinal regions, like sections of an orange. These regions map to four quadrants of the plane, representing the four possible combinations of the two divisions.
With an additional dimension, the plane also can be divided into points with positive values of y and points with negative values of y. These two halves of the plane are divided by the x-axis and correspond to the two hemispheres divided by the x-z plane. These two halves can be given various interpretations. For example, they can represent the distinction between singularity and plurality, manifesting in the world of objects the primordial distinction between One and Many. The two singular/plural hemispheres are orthogonal to the inner/outer hemispheres, dividing the sphere into four longitudinal regions, like sections of an orange. These regions map to four quadrants of the plane, representing the four possible combinations of the two divisions.
 The sphere has a reflection symmetry that exchanges positive and negative values of z, reflecting points in the upper hemisphere to points in the lower hemisphere, and vice versa. This exchanges subtle and gross realms of manifestation, and the same interpretation discussed in relation to the circle mandala applies to the sphere as well: degrees of subtlety are mirrored by degrees of concreteness, with higher concreteness corresponding to higher subtlety. In the plane this reflection exchanges a point at a distance r from the origin with a point at a distance 1/r from the origin, thus exchanging large for small and vice versa. In particular, the most concrete point at the origin is exchanged with the point at infinity, symbolizing the identity of emptiness and form.
The sphere has a reflection symmetry that exchanges positive and negative values of z, reflecting points in the upper hemisphere to points in the lower hemisphere, and vice versa. This exchanges subtle and gross realms of manifestation, and the same interpretation discussed in relation to the circle mandala applies to the sphere as well: degrees of subtlety are mirrored by degrees of concreteness, with higher concreteness corresponding to higher subtlety. In the plane this reflection exchanges a point at a distance r from the origin with a point at a distance 1/r from the origin, thus exchanging large for small and vice versa. In particular, the most concrete point at the origin is exchanged with the point at infinity, symbolizing the identity of emptiness and form.
 The spherical mandala suggests various alternative ways of dividing the sphere, resulting in many possible planar mandalas. The planar mandala with four quadrants and multiple levels arises by a particular symmetry-breaking of the sphere according to three coordinate axes. There are many other possible ways to break the symmetry of the sphere, however, and none is inherently privileged. For example, there are exactly five Platonic solids that break spherical symmetry in a way that corresponds to regular polyhedra. The octahedron with vertices aligned with the three axes naturally corresponds to the particular model we have illustrated above, with its eight faces corresponding to the eight regions of the sphere resulting from the equatorial division and the two longitudinal divisions. Its edges can be projected outward to the surface of the sphere, resulting in the two longitudinal divisions of the sphere and the equatorial division. These divisions are then projected as the x-axis and y-axis in the plane and the unit circle. Alternatively, one can discard the sphere and consider the mapping directly from the octahedron to the plane using the same map used for the sphere. Although this model retains all the reflection symmetries, it has the disadvantage that it no longer has the continuous rotational symmetry of the sphere.
The spherical mandala suggests various alternative ways of dividing the sphere, resulting in many possible planar mandalas. The planar mandala with four quadrants and multiple levels arises by a particular symmetry-breaking of the sphere according to three coordinate axes. There are many other possible ways to break the symmetry of the sphere, however, and none is inherently privileged. For example, there are exactly five Platonic solids that break spherical symmetry in a way that corresponds to regular polyhedra. The octahedron with vertices aligned with the three axes naturally corresponds to the particular model we have illustrated above, with its eight faces corresponding to the eight regions of the sphere resulting from the equatorial division and the two longitudinal divisions. Its edges can be projected outward to the surface of the sphere, resulting in the two longitudinal divisions of the sphere and the equatorial division. These divisions are then projected as the x-axis and y-axis in the plane and the unit circle. Alternatively, one can discard the sphere and consider the mapping directly from the octahedron to the plane using the same map used for the sphere. Although this model retains all the reflection symmetries, it has the disadvantage that it no longer has the continuous rotational symmetry of the sphere.
 The other Platonic solids can also be inscribed in the sphere to produce other mandalas when projected into the plane. To give just one example, the icosahedron can be inscribed in the sphere to produce a planar mandala with five-fold symmetry. Its twenty faces map to twenty distinct regions in the plane, producing a particularly beautiful and complex mandala exhibiting a five-pointed star. There are also other ways to break the symmetry of the sphere that do not correspond to Platonic solids (i.e., discrete subgroups of the spherical group).
The other Platonic solids can also be inscribed in the sphere to produce other mandalas when projected into the plane. To give just one example, the icosahedron can be inscribed in the sphere to produce a planar mandala with five-fold symmetry. Its twenty faces map to twenty distinct regions in the plane, producing a particularly beautiful and complex mandala exhibiting a five-pointed star. There are also other ways to break the symmetry of the sphere that do not correspond to Platonic solids (i.e., discrete subgroups of the spherical group).
 There are, however, some noticeable differences between the models. First of all, the AQAL planar mandala is not presented as mathematically equivalent to a single higher-dimensional sphere. The AQAL model is, however, sometimes described as a collection of concentric nested spheres, with the planar AQAL representation being a cross-section of this collection of nested spheres. Each concentric circle in the planar representation corresponds to an equator of a different concentric sphere. In contrast, in the integral sphere model, the nested circles in the plane do not correspond to equators of multiple nested spheres, but to lines of latitude on a single sphere, thus integrating them all. More generally, in the integral sphere mandala, a single sphere simultaneously encodes all levels and all quadrants in the plane, whereas the AQAL model requires multiple spheres. It should be noted that a single four-dimensional integral sphere maps to a three-dimensional space of infinitely nested concentric spheres (corresponding to "spheres of latitude" on the four-dimensional integral sphere). Wilber's nested spheres, therefore, can be seen as a special case of the spherical mandala as well.
There are, however, some noticeable differences between the models. First of all, the AQAL planar mandala is not presented as mathematically equivalent to a single higher-dimensional sphere. The AQAL model is, however, sometimes described as a collection of concentric nested spheres, with the planar AQAL representation being a cross-section of this collection of nested spheres. Each concentric circle in the planar representation corresponds to an equator of a different concentric sphere. In contrast, in the integral sphere model, the nested circles in the plane do not correspond to equators of multiple nested spheres, but to lines of latitude on a single sphere, thus integrating them all. More generally, in the integral sphere mandala, a single sphere simultaneously encodes all levels and all quadrants in the plane, whereas the AQAL model requires multiple spheres. It should be noted that a single four-dimensional integral sphere maps to a three-dimensional space of infinitely nested concentric spheres (corresponding to "spheres of latitude" on the four-dimensional integral sphere). Wilber's nested spheres, therefore, can be seen as a special case of the spherical mandala as well.
 This map can be visualized by drawing lines radiating out from the point (0,−1). Each line intersects the real number line at one point and intersects the circle at one point, forming a one-to-one correspondence between them. This set of lines is the projective space P1, where the horizontal line through (0,−1) which does not intersect the line corresponds to the point at infinity ∞. Another way to visualize the map is to imagine cutting the circle at its bottom, then pulling the two endpoints apart to straighten the circle into a line segment, then stretching the line segment to extend the two end points outward infinitely far.
This map can be visualized by drawing lines radiating out from the point (0,−1). Each line intersects the real number line at one point and intersects the circle at one point, forming a one-to-one correspondence between them. This set of lines is the projective space P1, where the horizontal line through (0,−1) which does not intersect the line corresponds to the point at infinity ∞. Another way to visualize the map is to imagine cutting the circle at its bottom, then pulling the two endpoints apart to straighten the circle into a line segment, then stretching the line segment to extend the two end points outward infinitely far.
 The additive inverse in R corresponds to reflection through the z-axis in S1, and the multiplicative inverse in R corresponds to reflection through the x-axis in S1. Moreover, the antipode corresponds to the additive inverse of the multiplicative inverse.
The additive inverse in R corresponds to reflection through the z-axis in S1, and the multiplicative inverse in R corresponds to reflection through the x-axis in S1. Moreover, the antipode corresponds to the additive inverse of the multiplicative inverse.
 Similarly, the reflection of (x,z) about the x-axis is (x,−z) and the corresponding point in R is φ(x,−z). Now by definition φ(x,−z)φ(x,z) = [x/(1−z)][x/(1+z)] = x2/(1−z2) = x2/x2 = 1. Thus φ(−x,z) = 1/φ(x,z) = 1/s.
Similarly, the reflection of (x,z) about the x-axis is (x,−z) and the corresponding point in R is φ(x,−z). Now by definition φ(x,−z)φ(x,z) = [x/(1−z)][x/(1+z)] = x2/(1−z2) = x2/x2 = 1. Thus φ(−x,z) = 1/φ(x,z) = 1/s.